Wavelet Noise Thresholding

The wavelet coefficients calculated by a wavelet transform represent change in the time series at a particular resolution. By looking at the time series in various resolutions it should be possible to filter out noise. At least in theory. However, the definition of noise is a difficult one. One of my colleagues commented once that "one person's noise is another's signal". In part this depends on the resolution one is looking at. One algorithm to remove Gaussian white noise is summarized in section 10.5, Chapter 10, of Wavelet Methods for Time Series Analysis by Percival and Walden. The algorithm is:

Calculate a wavelet transform and order the coefficients by increasing frequency. This will result in an array containing the time series average plus a set of coefficients of length 1, 2, 4, 8... The noise threshold will be calculated on the highest frequency coefficient spectrum (this is the largest spectrum).
Calculate the median absolute deviation on the largest coefficient spectrum. The median is calculated from the absolute value of the coefficients. The equation for the median absolute deviation is shown below:

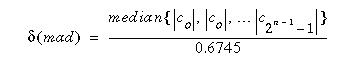
Here c₀, c₁, etc... are the coefficients.

The factor 0.6745 in the denominator rescales the numerator so that 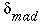is also a suitable estimator for the standard deviation for Gaussian white noise (Wavelet Methods for Time Series Analysis).
For calculating the noise threshold I have used a modified version of the equation in Wavelet Methods for Time Series Analysis. This equation has been discussed in papers by D.L. Donoho and I.M. Johnstone. This equation is shown below:

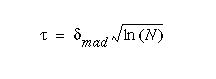
In this equation N is the size of the time series.
Apply a thresholding algorithm to the coefficients. There are two popular versions:
1. Hard thresholding. Hard thresholding sets any coefficient less than or equal to the threshold to zero.
```
  if (coef[i] <= thresh)
    coef[i] = 0.0;
  
```
2. Soft thresholding. Hard thresholding sets any coefficient less than or equal to the threshold to zero. The threshold is subtracted from any coefficient that is greater than the threshold. This moves the time series toward zero.
```
  if (coef[i] <= thresh)
    coef[i] = 0.0;
  else
    coef[i] = coef[i] - thresh;
  
```
I have used hard thresholding. Soft thresholding not only smooths the time series, but moves it toward zero. For my applications this is not a desirable property.

Ian Kaplan, August 2001
Revised:

Local links:
Applying the Haar Wavelet Transform to Time Series Information
Wavelets in Java