Signal Windowing to Reduce DFT Leakage

DFT of four period sin(x)

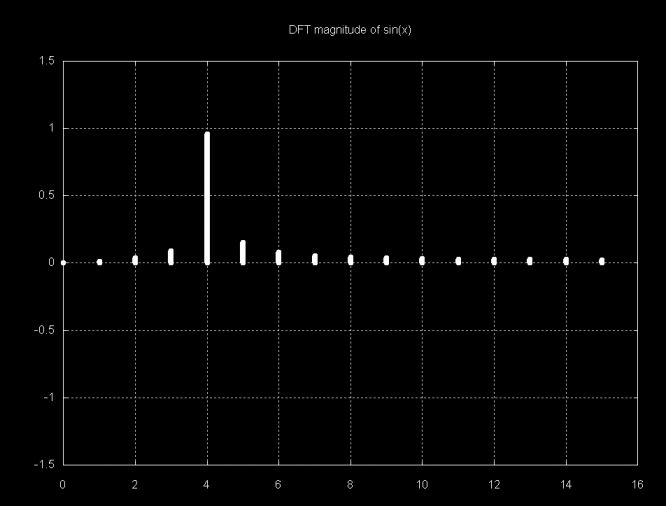
The magnitude graph of sin(x), above, exhibits the embarrassment of DFT leakage. Instead of having a signal magnitude 1.0 value at an x-axis location this case corresponds to the number of sin(x) periods, there is a magnitude that is slightly less than 1.0 and several sub-magnitudes. For sin(x) this is not a big problem, since it is easy to distinguish the major component of the signal. However, if it is a complex signal, which smaller components, the smaller components may be obscured by the DFT leakage.

One solution to the humiliating problem of DFT leakage is windowing. Lyons discusses three windowing functions:

1. Triangular window
2. Hanning window
3. Hamming window

These functions smoothly "tail off" the signal at both ends, reducing DFT leakage. Each point, s_i in the signal is multiplied by a window scaling factor w_i before the DFT is calculated. The effect of the window functions on an 8-period sin(x) signal is shown below:

8-period sin(x) signal, scaled with a triangle window

8-period sin(x) signal, scaled with a hanning window

8-period sin(x) signal, scaled with a hamming window

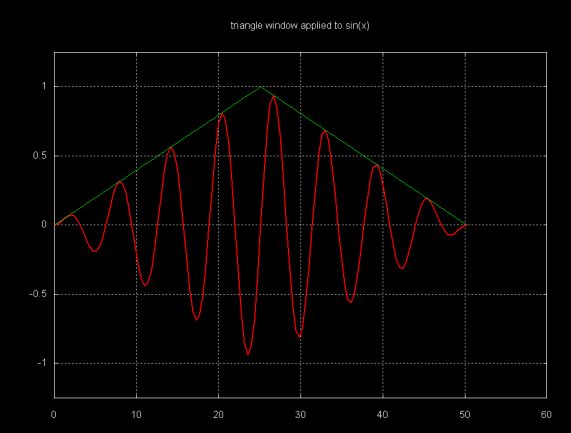
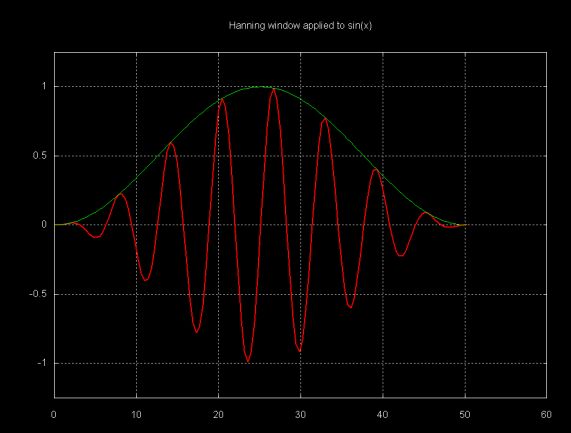
The Java window class (which is part of the fourier package) contains three methods which implement these window functions. This class can be downloaded here.

The graphs below show the DFT of a sample containing four periods of sin(x), where the three window functions have been applied to the sample before calculating the DFT.

DFT magnitude of a 4-period sin(x), scaled with a triangle window

DFT magnitude of a 4-period sin(x), scaled with a hanning window

DFT magnitude of a 4-period sin(x), scaled with a hamming window

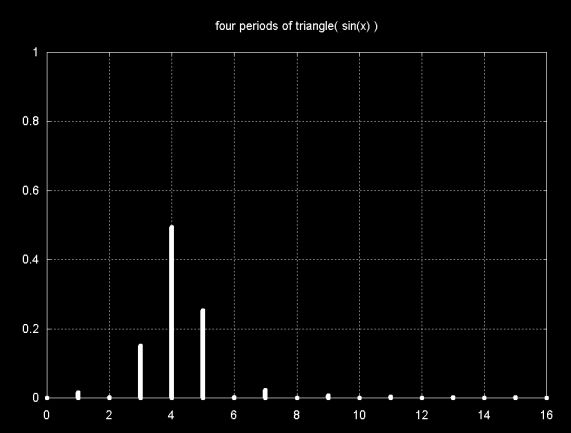
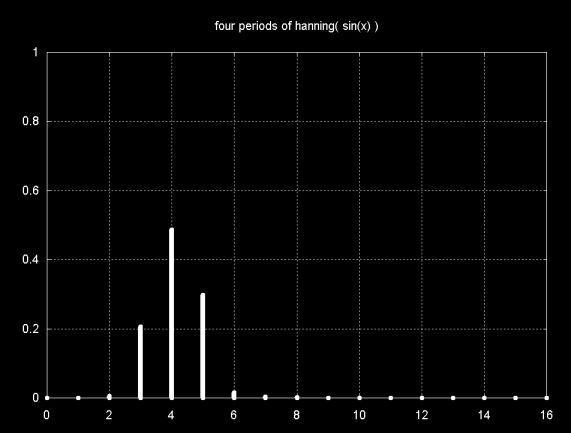
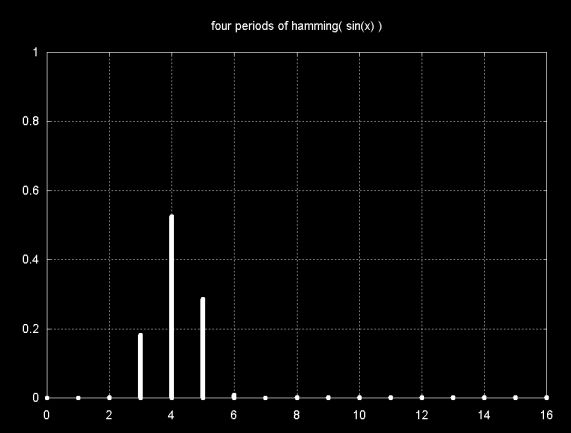
Since there are four sin(x) periods (cycles), the main magnitude line is at 4. The windowing functions reduce DFT leakage to close to zero in all three cases, except in the immediate vicinity of the sin(x) frequency. Note that the magnitude is also reduced from close to 1.0 to about 0.5.

Lyons shows how windowing can reduce DFT leakage that would otherwise obscure signal components. However, the opposite can also true. For two signals that are close to each other in frequency, where one signal is smaller than the other, windowing can obscure a signal component.

The graph below shows four periods of sin(x) + 0.5sin(1.2x).

signal(x) = sin(x) + 0.5sin(1.2x)

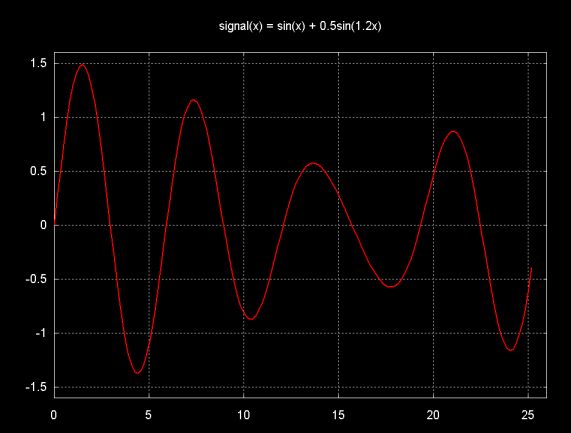
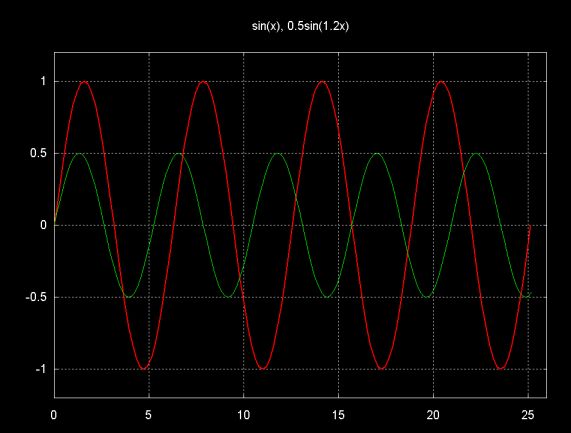
The signal above is composed of the addition of the two signals shown below.

sin(x), 0.5sin(1.2x)

The magnitude plot of the unwindowed DFT of the four period sample of sin(x) + 0.5sin(1.2x) is shown below. Note that there is one frequency component at 4 and one frequency component at 5. All other magnitudes are a result of DFT leakage.

DFT magnitude of 4-periods of the function sin(x) + 0.5sin(1.2x)

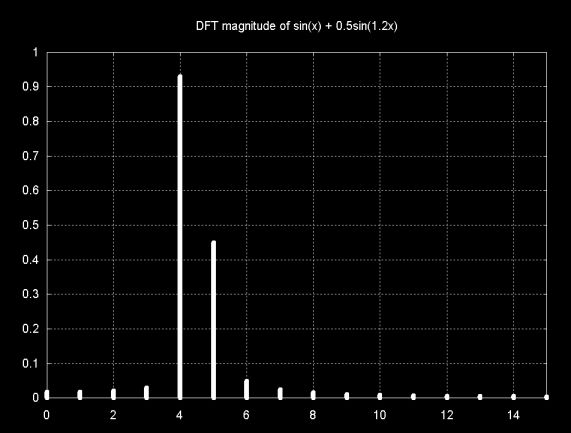
The DFT magnitude plot of the same signal, windowed with the Hamming window, is shown below. The DFT leakage magnitudes at the far ends of the graph are removed. However, the windowing artifact at frequency 3 is actually larger than the smaller signal component at frequency 5. In this case windowing actually obscures the smaller signal, by making it difficult or impossible to distinguish from the windowing artifacts.

DFT magnitude of 4-periods of the function sin(x) + 0.5sin(1.2x), scaled with the Hamming window

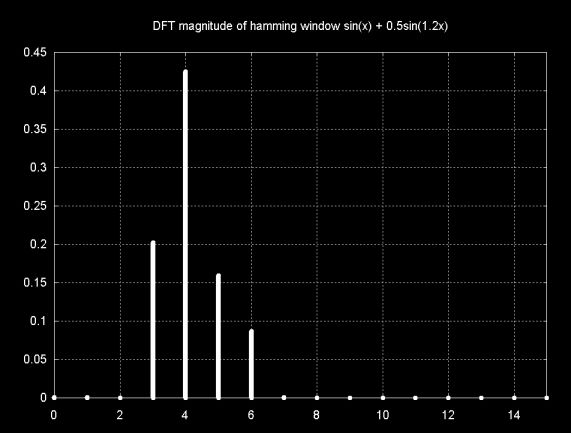
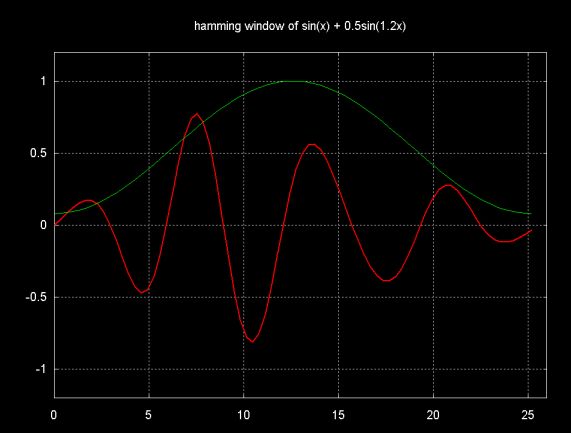
As the graph below shows, the Hamming window squashes the signal, which reduces the DFT resolution.

4-periods of the function sin(x) + 0.5sin(1.2x), scaled with the Hamming window

Increasing the number of periods within the window does not help. For example, using four times the number of periods for sin(x) + 0.5sin(1.05x) simply results in the same magnitude graph shifted by a factor of four. The problem is the closeness of the signals, not the number of periods within the window.

Ian Kaplan, September 2001
Revised:

Back to A Notebook Compiled While Reading Understanding Digital Signal Processing by Lyons